前言
Python 是当前图像处理领域的主打语言之一。在计算机视觉(特别是深度学习图片预处理、模型训练)等复杂度较高,技术迭代速度快的领域,用 Python 快速开发出算法原型、验证效果是许多研发人员的首选方案。著名图像处理库 OpenCV 就提供了完整的 Python 封装,用户可以书写 Python 调用底层的 C++ 实现来获得不错的性能。

理想很丰满,现实很骨感。在实际的研发任务中,仅仅使用 OpenCV 的 Python 接口往往是不够的:当某些处理算法 OpenCV 没有提供,需要用户亲自实现时,Python 的性能就比较尴尬了。图像通常是以 NumPy 数组的形式存储在内存中的,当需要逐个遍历像素处理时,Python 的 for 循环效率很低。在需要实时处理的场景(比如摄像头传回的画面)或者数据量较大的时候,Python 的解释器开销会是个很大的性能瓶颈。
Taichi 在这一点上恰好可以帮到大家:
- Taichi kernel 里的顶层 for 循环是自动并行的,用户无需分配和管理线程;
- Taichi 的即时编译 (JIT) 机制可以把 Taichi 代码编译成高效的机器码,并通过指定后端跑在多核 CPU 或 GPU 等不同的后端上,用户无需担心编译和环境适配;
- Taichi 可以在 CPU、GPU 执行中无缝切换,对于计算量特别大的部分可以一键切换到 GPU 计算;
- 在同一份程序中用户可以在调用 OpenCV 和调用自己的 Taichi 实现中来回切换,所有工作都在同一份 Python 程序中完成。这和在 Python 外独立写一份 C++/CUDA 代码再用 ctypes/pybind11 等工具桥接比起来,使用和移植都方便很多。
以上几点可以让用户在享受 Python 便利的同时,获得媲美 C++/CUDA 的运行效率。
本文接下来将通过三个篇章具体介绍如何使用 Taichi 加速 Python 图像处理:
- 入门篇:图像的转置与双线性插值;
- 进阶篇:高斯滤波器与双边滤波器;
- 入魔篇:双边网格与高动态范围色调映射 (Tone mapping)。
在这些内容中大家可以看到这些图像处理算法是如何一步步被改进的,以及它们的一些有趣应用。
在文末我们会讨论使用 Taichi 进行图像处理的注意事项,以及 Taichi 目前还存在哪些局限、不足,可以在未来改进。
在开始正文之前,请大家确保自己的机器上已经安装了最新版本的 Taichi 和 opencv-python 这个库:
pip3 install -U taichi opencv-python本文的所有代码都放在 GitHub 上:Image processing with Taichi.
入门:图像的转置与插值
图像的转置
我们从一个最简单的例子开始,帮助大家了解使用 Taichi 进行处理图像的基本步骤:图像的转置。
图像的转置与矩阵的转置类似,就是把图像 和
位置的像素交换位置 (transpose):

我们首先导入所要使用的库,并调用 ti.init() 做一些初始化。这对每个 Taichi 程序来说都是必不可少的:
import cv2
import numpy as np
import taichi as ti ti.init()把小猫的图像读入内存:
src = cv2.imread("./images/cat.jpg")
h, w, c = src.shape
dst = np.zeros((w, h, c), dtype=src.dtype) img2d = ti.types.ndarray(element_dim=1) # Color image type绝大多数 Python 图像处理库都假定图像具有 NumPy 的数组形式,OpenCV 也是如此。对灰度图像(单通道)对应的数组是二维的,形状是 (height, width),彩色图像(多通道)对应的数组是三维的,形状是 (height, width, channels)。上面的代码中 OpenCV 读进来的图片 src 是一个三维 NumPy 数组,随后我们声明了一个数据类型与 src 相同,但长度和宽度与 src 交换的数组 dst 用于存放转置后的图片。
我们用下面这个函数 transpose 来处理图像的转置。从外表上看它和普通的 Python 函数没有什么两样,只不过开头加了一个装饰器 ti.kernel,所以是一个 Taichi kernel 函数:
@ti.kernel
def transpose(src: img2d, dst: img2d): for i, j in ti.ndrange(h, w): dst[j, i] = src[i, j]这个 kernel 很短,不过有两点值得说道:
- 在上面第二行代码中
src,dst分别表示传入和输出的图像,它们都使用了img2d = ti.types.ndarray(element=1)作为类型标注。Taichi 允许你通过ti.types.ndarray()将一个 NumPy 数组作为参数传入 kernel,参数element_dim的具体含义读者可以暂时不用关心,只要知道它的目的是让我们可以同时操作像素的 RGB 三个分量。这种传参方式传递的是数组的指针,不会有额外的拷贝(注:如果在 GPU 上运行则会有 CPU/GPU 之间的自动数据转移),kernel 内部对数组的修改同样也会在外部生效。 for i, j in ti.ndrange(h, w):这句是一个顶层的 for 循环,它会自动并行遍历处理数组的所有元素。其中i遍历图像的所有行,j遍历图像的所有列。
好了,我们只要调用这个 kernel 并将 dst 保存为图片:
transpose(src, dst)
cv2.imwrite("cat_transpose.jpg", dst)就可以看到输出的转置图片。
本例子的代码地址:image_transpose.py.
双线性插值
图像转置这个操作未免太过简单,我们再来看一个稍微复杂一点的例子:图像的双线性插值。
双线性插值是图像上采样 (upsampling) 中常用的手段。假设我们的小猫图片只有 96×64 像素,我们想把它放大 5 倍变成一张 480×320 的图像。直接粗暴地将每个像素变成一个 5×5 的 “马赛克” 可不是个好主意:


这是因为对放大后的图像中的某个像素 ,它在原图像中对应的位置
不见得正好落在原图像的某个像素上,直接取整或者四舍五入到最近的像素上,会导致图像看起来不太平滑。
双线性插值则是考虑了 周围的四个像素,将它们的像素值加权平均作为
的像素值返回:(图片来自维基百科)
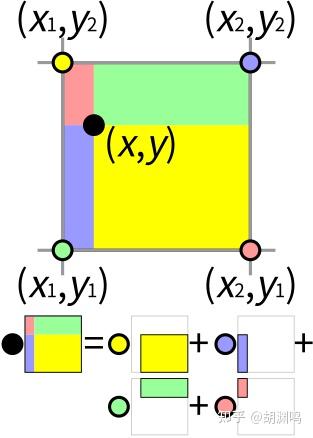
在上图中, 周围的四个像素
构成一个单位正方形,四个小矩形的面积之和是 1,每个像素对应的权重系数是与它颜色相同的矩形的面积。比如当 越靠近左上角黄色的点
时,右下方黄色矩形的面积就会越大,从而
像素获得的权重也就越大。
这个计算可以用三个一维的线性插值来得到:首先分别对 和
用权重
各作一次一维插值,然后把两个结果用权重
再作一次一维插值:
import taichi.math as tm @ti.kernel
def bilinear_interp(src: img2d, dst: img2d): for I in ti.grouped(dst): x, y = I / scale x1, y1 = int(x), int(y) # Bottom-left corner x2, y2 = min(x1 + 1, h - 1), min(y1 + 1, w - 1) # Top-right corner Q11 = src[x1, y1] Q21 = src[x2, y1] Q12 = src[x1, y2] Q22 = src[x2, y2] R1 = tm.mix(Q11, Q21, x - x1) R2 = tm.mix(Q12, Q22, x - x1) dst[I] = ti.round(tm.mix(R1, R2, y - y1), ti.u8) # Round into uint8在上面的代码中,我们用一个二维下标 I 遍历输出图像 dst 的所有像素,I 表示像素在 dst 中的行和列。I/scale 返回的是像素在原图 src 中的坐标 。
是像素
在
方向上的插值,
是像素
在
方向上的插值,
在
方向上再插值一次就得到了最终的像素值。
其中一维插值我们使用的是来自 taichi.math 模块的 mix 函数,定义如下:
@ti.func
def mix(x, y, a): # also named "lerp" in other libraries return x * (1 - a) + y * a最终的结果如下所示:


对比可见双线性插值给出的效果更为平滑。
本例子的代码地址:image_bilinear_inpterpolation.py.
进阶:高斯滤波器与双边滤波器
高斯滤波 (Gaussian filter)
高斯滤波是图像处理中常用的滤波算法之一,其作用是去除图像中的高频信息,使得图像变得模糊、平滑。高斯滤波是用一个矩阵与 2D 图像做卷积,这个矩阵叫做高斯核,它的元素来自二维高斯分布的采样。
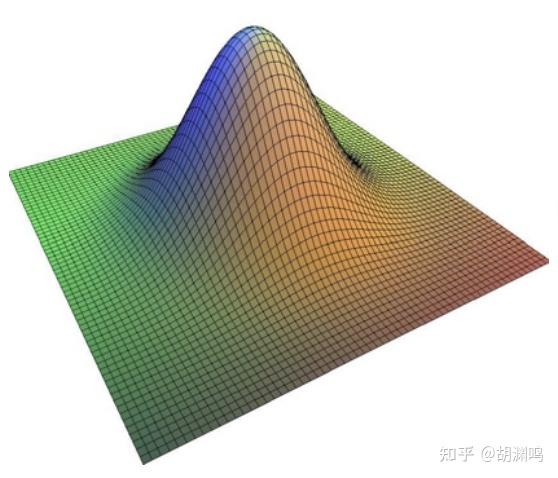
二维高斯分布的概率密度函数为
对一个 的高斯核
,其元素来自
在
这些点的采样,比如 3×3 的高斯核是这样的:
由于 是两个一维密度函数的乘积,所以高斯核是可分的,
可以写成一维向量
与自身转置的乘积:。这种情形图像与
的二维卷积可以分解为两个一维卷积:先对图像的每一列用
做一次一维卷积,然后对结果的每一行用
再做一次一维卷积(证明见这个网页)。这样就把二维卷积的复杂度从
减少到了
。

我们首先开辟一个 1D field (即一维数组)用于存放 1 维的高斯核:
weights = ti.field(dtype=float, shape=1024, offset=-512)这个 field 的长度是 1024,在绝大多数场景下肯定够用了。注意到选项 offset=-512 表示这个 field 的下标是从 -512 开始的,到 511 为止。这是 Taichi 提供的 field 的 offset 功能,好处是下标范围关于原点是对称的,这样可以简化代码。我们用一个 @ti.func 来初始化这个 field:
@ti.func
def compute_weights(radius: int, sigma: float): total = 0.0 ti.loop_config(serialize=True) for i in range(-radius, radius + 1): val = ti.exp(-0.5 * (i / sigma)**2) weights[i] = val total += val ti.loop_config(serialize=True) for i in range(-radius, radius + 1): weights[i] /= total其中参数 radius 控制高斯核的大小:高斯核中实际使用的元素下标范围为 [-radius, radius],sigma 是 Gauss 密度函数的方差。
这里值得注意的是我们使用了 ti.loop_config(serialize=True) 关闭了紧随其后的 for 循环的并行。这是因为在计算量比较小的情形,在 CPU/GPU 上生成大量线程的开销可能反而占了大头,所以我们让 for 语句串行执行即可。计算高斯核每个元素时,可以不用关心系数 ,最后用
total 变量统一做归一化。
接下来我们来计算两次实际的一维卷积。我们开辟一个尺寸为 1024×1024 的 Vector Field (其实就是元素是 RGB 的二维数组) 用于存储第一次滤波后的中间图像:
img = cv2.imread('./images/mountain.jpg')
img_blurred = ti.Vector.field(3, dtype=ti.u8, shape=(1024, 1024))然后先对列、再对行分别做一维滤波:
@ti.kernel
def gaussian_blur(img: img2d, sigma: float): img_blurred.fill(0) blur_radius = ti.ceil(sigma * 3, int) compute_weights(blur_radius, sigma) n, m = img.shape[0], img.shape[1] for i, j in ti.ndrange(n, m): l_begin, l_end = max(0, i - blur_radius), min(n, i + blur_radius + 1) total_rgb = tm.vec3(0.0) for l in range(l_begin, l_end): total_rgb += img[l, j] * weights[i - l] img_blurred[i, j] = total_rgb.cast(ti.u8) for i, j in ti.ndrange(n, m): l_begin, l_end = max(0, j - blur_radius), min(m, j + blur_radius + 1) total_rgb = tm.vec3(0.0) for l in range(l_begin, l_end): total_rgb += img_blurred[i, l] * weights[j - l] img[i, j] = total_rgb.cast(ti.u8)在代码 3-5 行处,我们先将滤波后的图像置为 0,并初始化了高斯滤波器。接下来 7-14 行和 16-22 行的两个 for 循环分别是对列、行的一维滤波,它们本质上是一样的,只不过第一个循环会将列滤波的结果存在 img_blurred 中,第二个循环将结果写回原图像 img。第一个 for 循环中 img_blurred[i, j] 的值就是将滤波器竖起来覆盖在 img 上,使得其中心位置与 img[i, j] 重叠,然后计算滤波器的所有元素与其下方 img 元素乘积之和。就是这么简单!
本例子的代码地址:gaussian_filter_separate.py.
双边滤波器 (Bilateral Filter)
高斯滤波器总是用固定的权重计算,所以虽然它会让图像变得平滑,但同样也会丢失图像的一部分细节。比如某些边缘的部分会模糊掉。
那有没有什么办法,可以在保持图像边缘细节的同时实现平滑呢?既然高斯滤波器的权重只与像素之间的距离有关,何不再加入一个依赖于像素值差的权重因子呢?这就是双边滤波的思路:
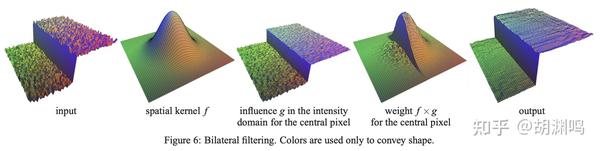
上图中,我们将一个 2D 灰度(单 channel)图像 plot 到 3D 空间,其中高度就是像素的值。可以看到,双边滤波器可以在保持“悬崖”(即图像中的边缘)的同时,光滑两边的“山坡”。
其中 是上一小节中基于像素距离的高斯核,
是新引入的基于像素差距的高斯核:
是归一化系数。所以在计算
位置像素的滤波时,来自像素
的权重贡献为
从而两个像素的差 越大,在计算滤波时
贡献的值就越小,从而起到了保持边缘的效果:

双边滤波器不是可分的,它不能分解成两个一维卷积,所以我们只能老老实实写二维卷积了:
img_filtered = ti.Vector.field(3, dtype=ti.u8, shape=(1024, 1024)) @ti.kernel
def bilateral_filter(img: img2d, sigma_s: ti.f32, sigma_r: ti.f32): n, m = img.shape[0], img.shape[1] blur_radius_s = ti.ceil(sigma_s * 3, int) for i, j in ti.ndrange(n, m): k_begin, k_end = max(0, i - blur_radius_s), min(n, i + blur_radius_s + 1) l_begin, l_end = max(0, j - blur_radius_s), min(m, j + blur_radius_s + 1) total_rgb = tm.vec3(0.0) total_weight = 0.0 for k, l in ti.ndrange((k_begin, k_end), (l_begin, l_end)): dist = ((i - k)**2 + (j - l)**2) / sigma_s**2 + (img[i, j].cast( ti.f32) - img[k, l].cast(ti.f32)).norm_sqr() / sigma_r**2 w = ti.exp(-0.5 * dist) total_rgb += img[k, l] * w total_weight += w img_filtered[i, j] = (total_rgb / total_weight).cast(ti.u8) for i, j in ti.ndrange(n, m): img[i, j] = img_filtered[i, j]这个过程和高斯滤波是一样的,区别在于我们只需要用一个 for 循环并行处理所有像素,用 total_weights 统计所有来自高斯核覆盖的像素权重,用 total_rgb 统计这些像素值的加权和,最后做归一化处理。
应用:用双边滤波器进行磨皮美颜
双边滤波器有着广泛的应用,最典型的就是图像降噪 (denoising)、图像平滑 (image smoothing) 等,而后者是一种经典的磨皮美颜算法:
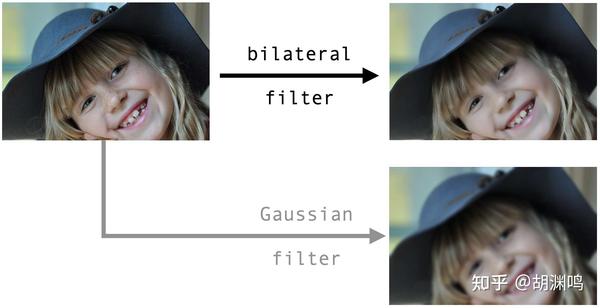
可以看到,双边滤波器可以在保持图片中锐利边缘的同时,抹去局部细节,起到磨皮效果。我还放了一张相同半径的高斯滤波器对比,可以看到高斯模糊会模糊边缘,效果是无法接受的。(输入图片来源:Pixarbay)
本例子的代码地址:bilateral_filter.py.
入魔:双边网格(Bilateral Grid)
双边滤波器的性能问题
双边滤波虽然能够在保持边缘的同时实现平滑,但它的性能是个很大的问题。前面提到 2D 的高斯滤波器可以通过分解为两个 1D 的高斯滤波解决,甚至对于较大的卷积核更有快速傅里叶变换 (FFT) 进一步提升性能,但双边滤波器就没有这种福分了:它不是可分的,无法表示成两个独立的 1D 卷积;由于依赖图像内容,所以也不能使用 FFT。
那么有没有什么办法可以改造双边滤波器,使得它是可分的呢?答案是有的,这就是下面要介绍的双边网格 (Bilateral Grid) 滤波。
双边网格 (Bilateral Grid) 出自论文 Chen et al., SIGGRAPH 2007,是双边滤波器的加速版本。这个方法非常精彩,是一个通过提升维度来简化问题的范例。它包含一系列操作步骤,所以乍看起来会有点复杂,但我向你保证它背后的想法是很简单的。
八卦一下:这篇文章的 last author 是我的 Ph.D. 导师 Fredo Durand,第一作者 Jiawen Chen 在是大我十几届,没有照过面的 MIT 师兄,第二作者 Sylvain Paris 是 Adobe 著名研究员,当年是 Fredo 的 post-doc。Fredo 真是从真实感渲染、计算摄影到编译器啥都能搞,太能打了…
双边网格的核心想法是通过维度提升使得双边滤波可分。双边滤波不可分的原因是卷积核里面带有图像的像素值,如果把这个像素值的部分作为第三个维度上的独立卷积,不就可以实现可分了吗?
比如以灰度图像为例,图像是一个二维网格 ,每个元素存储的是像素的灰度值。我们把这个二维网格提升为一个三维网格
,第三个维度的长度是灰度的范围 [0, 255],从而整个网格大小为
。网格的
位置的元素存储的值如下:
对这个三维网格做三维的高斯滤波,假设得到的结果是三维网格 ,则
就是所求的对
双边滤波后的结果。
这里有个技巧值得注意:网格存储 这个二元组是为了在卷积时用第一个位置记录像素值的加权和
,用第二个位置记录权重的和
,最后相除就得到了归一化的结果。
下图是原论文中给出的一维提升到二维的例子,包含三个步骤:网格创建 (create),网格处理(process)、网格切片(slice)。
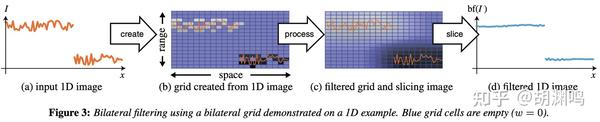
上图中最左边输入的是一维的信号,它的两段之间有一个明显的间断(即边缘)。提升为二维网格(左边第二张图)后,它们变成图像中两个不连通的区域。如果对这个图像作二维的高斯滤波的话,由于两个区域间断处的像素距离比较远,所以它们在滤波时给对方贡献的权重很小,甚至没有,所以双边网格是可以保持边缘信息的。当然,上面这张图是为了画图简便,采用了一维信号作为输入,所以 Grid 是二维的;在我们的情况中,输入是二维的,Grid 就是三维的。
在具体实现中,由于对一张 1024×1024=1MB 的灰度图,升维后网格的大小是 1024x1024x256=256MB,占据的空间实在是有点大,而且我们要的本来就是滤波后的结果,维护一个精确的大网格没有必要,所以我们会按比例缩小创建的网格(降采样),然后在滤波后再超采样回去。
具体步骤和代码介绍如下,我们采用灰度图像作为输入。
第一步:Create, 创建网格(降采样与升维)
我们首先声明两个 VectorField 用于存储三维网格及其滤波的中间结果,大小固定为 512x512x128 (32MB)。再声明一个形状是 2×512 的 field 用于存储滤波器的系数,2 表示有两个滤波器,一个给图像的空域 (spatial space),一个给像素的值域 (range space)。
grid = ti.Vector.field(2, dtype=ti.f32, shape=(512, 512, 128))
grid_blurred = ti.Vector.field(2, dtype=ti.f32, shape=(512, 512, 128))
weights = ti.field(dtype=ti.f32, shape=(2, 512), offset=(0, -256))我们省略初始化 weights 的代码部分,这个和之前高斯滤波器中的步骤是完全类似的。初始化 grid 的代码如下:(以下代码在 kernel 内执行)
grid.fill(0)
for i, j in ti.ndrange(img.shape[0], img.shape[1]): lum = img[i, j] grid[ti.round(i / s_s, ti.i32), ti.round(j / s_s, ti.i32), ti.round(lum / s_r, ti.i32)] += tm.vec2(lum, 1) grid_blurred.fill(0)
grid_n = (img.shape[0] + s_s - 1) // s_s
grid_m = (img.shape[1] + s_s - 1) // s_s
grid_l = (256 + s_r - 1) // s_r其中 s_s 是图像大小的缩放因子,s_r 是值域 [0, 255] 的缩放因子。grid_blurred 初始化为 0。
顺便我们计算了缩放后的三维网格的实际大小 grid_n, grid_m, grid_l。
第二步:Process, 网格操作(高斯模糊等)
现在我们可以对三维网格 grid 做三维高斯滤波了。这一步代码看似很长,其实反而是最简单的部分,因为它不过是我们前面介绍过的高斯滤波部分的重复,只是多了一次滤波。
注意经典的 Bilateral filter 算子在这一步变成了三个可分 filter:(以下代码均在 kernel 内执行)
blur_radius = ti.ceil(sigma_s * 3, int)
for i, j, k in ti.ndrange(grid_n, grid_m, grid_l): l_begin, l_end = max(0, i - blur_radius), min(grid_n, i + blur_radius + 1) total = tm.vec2(0, 0) for l in range(l_begin, l_end): total += grid[l, j, k] * weights[0, i - l] grid_blurred[i, j, k] = total for i, j, k in ti.ndrange(grid_n, grid_m, grid_l): l_begin, l_end = max(0, j - blur_radius), min(grid_m, j + blur_radius + 1) total = tm.vec2(0, 0) for l in range(l_begin, l_end): total += grid_blurred[i, l, k] * weights[0, j - l] grid[i, j, k] = total blur_radius = ti.ceil(sigma_r * 3, int)
for i, j, k in ti.ndrange(grid_n, grid_m, grid_l): l_begin, l_end = max(0, k - blur_radius), min(grid_l, k + blur_radius + 1) total = tm.vec2(0, 0) for l in range(l_begin, l_end): total += grid[i, j, l] * weights[1, k - l] grid_blurred[i, j, k] = total这一段包含三个顶层的 for 循环,前两个是对空间滤波,使用的权重来自 weights[0];第三个是对值域滤波,使用的权重来自 weights[1]。
我们把每次滤波的结果轮流写入 grid_blurred 和 grid。三轮滤波后最终的结果存储在 grid_blurred 中。
第三步:Slice, 网格切片(三线性插值)
最后我们来从“缩水”的网格 grid_blurred 中超采样获得滤波后的图像。这一步同样非常简单:(以下代码同样需要在 kernel 内执行)
for i, j in ti.ndrange(img.shape[0], img.shape[1]): lum = img[i, j] sample = sample_grid(i / s_s, j / s_s, lum / s_r) img[i, j] = ti.u8(sample[0] / sample[1])首先我们定位到未缩水的完整三维网格的 [i, j, img[i,j]] 处,这里的网格值可以根据缩水后的网格在 [i / s_s, j / s_s, lum / s_r] 处的值用一个插值函数 sample_grid 得出来,得到的结果是一个二元组 ,
是像素的加权和,
是权重的和,二者相除即为滤波后的值。
插值函数 sample_grid 是个啥?读者不难想到,它正是我们之前介绍的双线性插值的升维版本:三线性插值。和双线性插值类似,三线性插值对应的是单位正方体八个顶点的加权和。它可以通过先在正方体上下两个表面分别做一次双线性插值,然后将两个结果再做一次线性插值得到。
本例子的代码地址:bilateral_grid.py.
总结一下: 通过把 2D 图像升级到 3D,我们用一个 3D 可分卷积代替了一个 2D 的不可分 “卷积”。这样做会有性能优势吗?我们来分析一下:
- 3D 网格的 x, y 分辨率其实比原图低很多,所以整个 3D 网格的 “体素” 数目其实不见得就比 2D 图像的像素多。
- 另一方面,本来非常昂贵的不可分 2D 卷积被拆分成了可分的三次卷积,计算量大幅下降。
- 当然,整个系统的另一大亮点是非常 GPU 友好,特别是使用 Taichi 实现的时候 🙂
应用:实时 Local Tone Mapping(“HDR” 效果)
人眼能够感知到的动态范围,即最亮和最暗光强的比值,能够达到 ,但是普通显示设备上只能做到
,而比较好的摄影器材的动态范围则在显示器和人眼之间。不经处理地将高动态范围(High dynamic range, HDR)的图片在低动态范围 (Low Dynamic Range, LDR) 的设备上显示就会造成很多尴尬,难以同时展示图片亮部和暗部的细节:

色调映射(Tone mapping)是解决这个问题的良药。Tone mapping 有两种,一种是对屏幕上所有的像素用同一个函数调整亮度,即 Global tone mapping;另一种则会根据每个像素周围的像素智能地根据上下文 (context) 进行调整亮度,即 Local tone mapping,往往更为有效。
而 Local tone mapping 和 Bilateral filter 有什么联系呢?不难想到 Bilateral filter 最大的优势就在于 “保留边缘,抹去局部细节”,而 Local tone mapping 的需求恰恰是 “去掉边缘,保留局部细节”。由于人眼对于局部细节更为敏感,反向的 Bilateral filter,如果用在图片的亮度上,就可以有效压缩 HDR 图片的动态范围,便于在 LDR 设备上显示。Bilateral filter 用于局部色调映射的具体步骤如下:
- 对 RGB 的图片计算 log luminance(R、G、B 的加权求和后,取对数),称此图为
;
- 对 log luminance 图片
进行 bilateral filtering,得到光滑后的 log luminance base 图片,即
bilateral_filter
;
- 计算亮度细节 (detail) 图层
,这一部分是我们希望保留的亮度细节;
- 将 B 进行压缩,
,其中
。(这部分是动态范围过大的罪魁祸首,且压缩这部分不影响人眼对内容的感知);
- 重新计算调整后的 log luminance
,其中
是曝光补偿常数;
- 利用
计算新的图片,确保每个像素的 RGB 和原来保持比例,而 luminance 符合
的结果。
运行 Bilateral Grid tone mapping 以后,结果终于舒服了,能同时看到高光和阴影处的结果。

这部分的代码在 bilateral_grid_hdr.py.
著名游戏《对马岛之魂》中就用到了双边网格进行色调映射,实现了在 PS 4 上 1080 分辨率只需要 250 us 就能完成相关处理(等我有空了一定要去玩一下这个游戏,“实地调研”一下):

图片来源:SIGGRAPH 2021 Advances in Real-Time Rendering: Real-Time Samurai Cinema: Lighting, Atmosphere, and Tonemapping in Ghost of Tsushima(YouTube 有视频,这个老哥讲得特别好,非常完整地 cover 了对马岛之魂的后处理管线的各种细节,建议有兴趣的同学观看一下。听说知乎上贴 YouTube 链接不太好,我就不放了,不过很容易搜索到。)
注意事项
- 存储与可视化:因为一些历史原因,OpenCV 中默认的 channel 存储顺序为 BGR,这一点尤其要注意。Taichi 的可视化系统中采用 RGB 顺序。另外,OpenCV 的可视化工具
imshow等将图片的左上角作为(0, 0),纵向为 i,横向为 j;而 Taichi 的gui.set_image的坐标系会将左下角作为(0, 0),横向为 i,纵向为 j。当然,如果只是用 Taichi 进行计算而不是显示,i、j 的顺序并没有这么重要,本文中也没有仔细区分。 - 调试模式:在 Taichi 中,在
ti.init里面打开debug=True可以进入调试模式,这时程序性能会微微下降,但是会自动检查数组越界等常见错误,大大方便调试。这一点是 CUDA 等工具不具备的。 - 数据类型:图片常常被
np.uint8等格式保存,对应的 Taichi 格式是ti.u8。类似地,np.float32对应 Taichi 的ti.f32,或者直接使用float也行。 - 关于性能:如果对于特别分辨率小的图片,使用 Taichi 在 GPU 上运算时可能并没有加速,因为 GPU kernel 的启动、Taichi 的 JIT 编译时间、以及 pybind11 的开销会抵消加速。而对于规模比较大的图片、复杂的计算,往往加速会比较明显。
结语
Taichi 是否可以在加速图像处理上有独特优势?答案是肯定的,我想很多读者应该也会和我一样得到相同的结论:对于 Bilateral Grid 这样的经典算法,用别的工具在 Python 中用 GPU 高效实现,是相当困难的。当然,在写作本文的过程中,我也发现了 Taichi 的很多不足之处,好在其中的大部分是比较容易在未来修复的。比如:
ti.types.ndarray(element_dim=1)等 API 过长,对于用户来说需要记忆的 API 量还比较大;- 在开发完原型后,用户常常有部署的需求,而这一块需要使用 Taichi 正在开发的 AOT 功能来支持;
- Pybind11 造成的调用开销对于小规模图像计算可能会导致性能下降;
- 与 Matlab 等工具相比,Taichi 在一些简单而经典操作上其实并不能带来生产力的提升:高斯模糊在 Matlab、OpenCV 里也许一行代码就能实现。Taichi 的强项还是在可定制性。当然,也许这些常用操作未来也会以某种形式进入 Taichi 之中;
- 还有一些报错不够响亮的问题,我直接在 GitHub 开 issue 了:https://github.com/taichi-dev/taichi/issues/6305。
即使目前的 Taichi 版本在图像处理任务中还稍稍有一些不顺手的地方,我们已经能够看到 Taichi 为图像处理用户带来独特的价值。随着相关问题在开源社区得到修复,我们相信 Taichi 一定能够在这个领域大放异彩。
本文所有代码均可以直接运行,输入图片也附在仓库内了。欢迎大家试玩:https://github.com/taichi-dev/image-processing-with-taichi
由于篇幅限制,本文并未对实际程序运行性能进行严谨的讨论,程序并未精心优化,也没有提及这些程序应该如何应用 Taichi AOT 部署到移动设备上。如果大家有兴趣,欢迎留言,等下次有机会的时候 (???),我再写长文介绍!
最后,对加速 Python、图像处理感兴趣的同学,欢迎在「太极图形」微信号回复 “加群“,与社区同学一起讨论呀!
参考文献与扩展阅读
- MIT 的双边滤波教程:https://people.csail.mit.edu/sparis/bf_course/
- Bilateral Grid 原始论文: https://people.csail.mit.edu/sparis/publi/2007/siggraph/Chen_07_Bilateral_Grid.pdf
- 《对马岛之魂的》实时后处理:SIGGRAPH 2021 Advances in Real-Time Rendering: Real-Time Samurai Cinema: Lighting, Atmosphere, and Tonemapping in Ghost of Tsushima
- 知乎上的一篇很棒的双边滤波中文教程:https://zhuanlan.zhihu.com/p/365874538
- Taichi 语言中文官网:https://taichi-lang.cn/
- Taichi 中文论坛:https://forum.taichi.graphics/
- Taichi 语言文档(部分有中文翻译):https://docs.taichi-lang.org/
- 本文中的部分图片来自 Wikipedia
本文作者:Yuanming & Liang